Visualizations of Parallel Delaunay Triangulation
In a Delaunay triangulation, no circumcircle contains another point. Delaunay triangulations have a lot of applications: for example, in graphics, to produce “nice” meshes which avoid skinny triangles.
Parallel algorithms for Delaunay triangulation are usually terribly complex. More recently, a beautifully simple algorithm was presented at SPAA’16 in the paper Parallelism in Randomized Incremental Algorithms. We’ll refer to this algorithm as BGSS for short, named after its authors: Guy Blelloch, Yan Gu, Julian Shun, and Yihan Sun. In this post, I’d like to give some intuition for how their algorithm works.
The BGSS algorithm is based on a classic incremental algorithm, commonly called rip-and-tent. To insert a point, you “rip” out some triangles, and then make a “tent” inside the resulting cavity.
For example below, we begin with a mesh and insert a new point. The set of ripped triangles is highlighted in blue, and then tent of the new point is drawn in red.
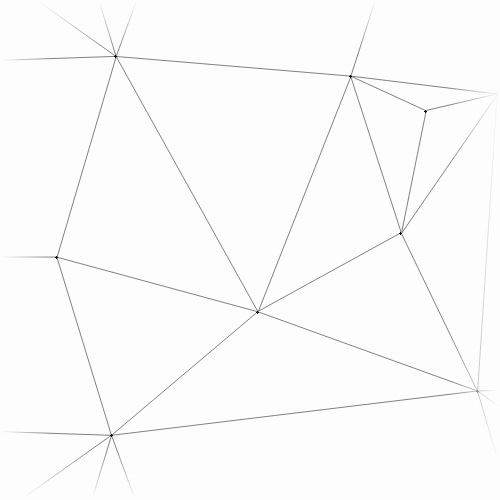 before before |
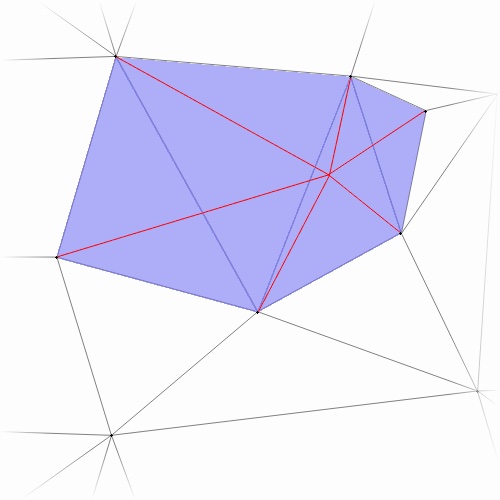 rip-and-tent rip-and-tent |
 after after |
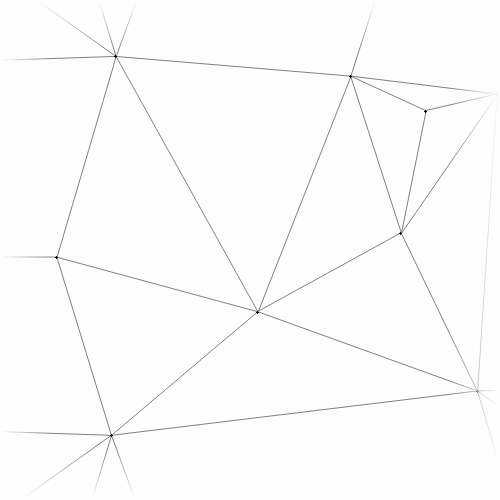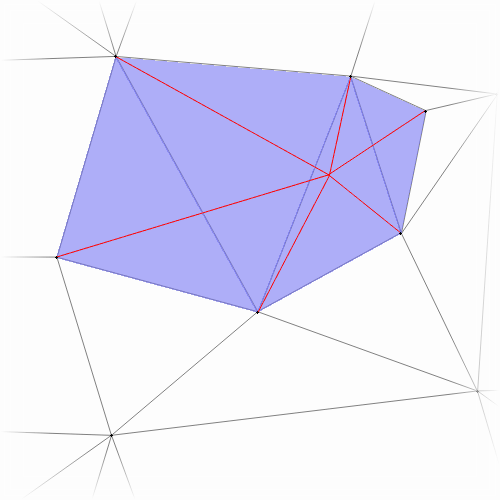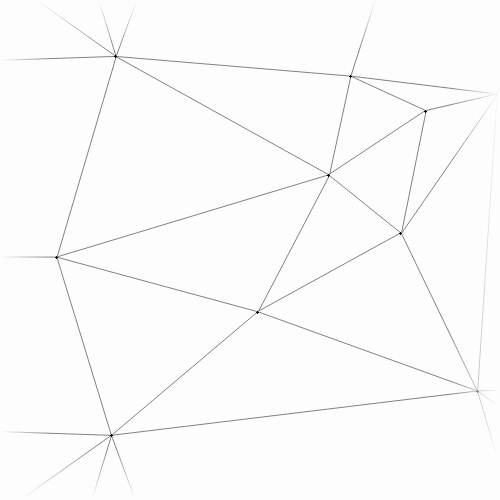
If we tried to insert multiple points simultaneously, the cavities created by these points might overlap, and we wouldn’t be able to build tents without resolving conflicts somehow. The classic incremental algorithm is therefore is entirely sequential: \(N\) points are inserted one after another, taking \(N\) steps total.
However, when inserting multiple points simultaneously, the cavities don’t always overlap:
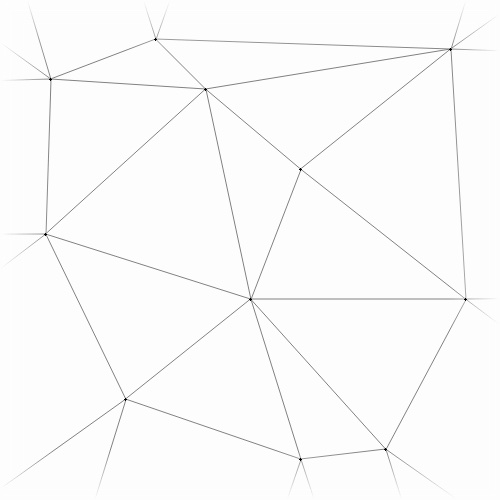 before before |
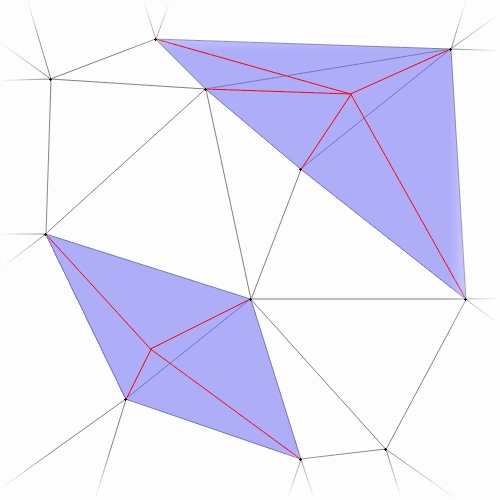 rip-and-tent rip-and-tent |
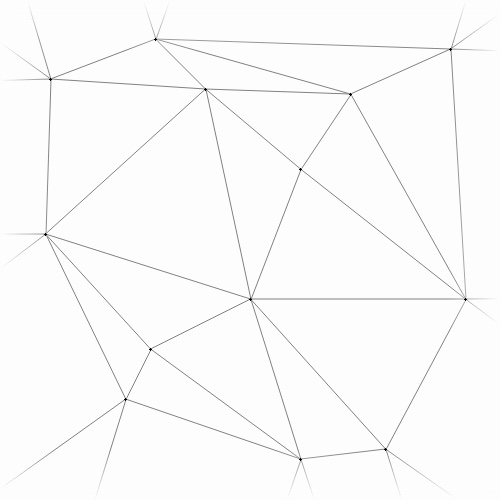 after after |
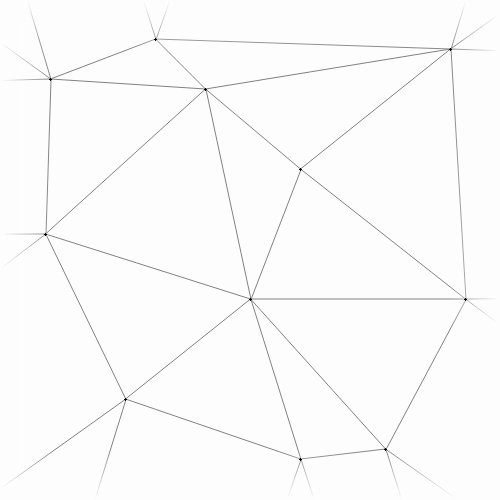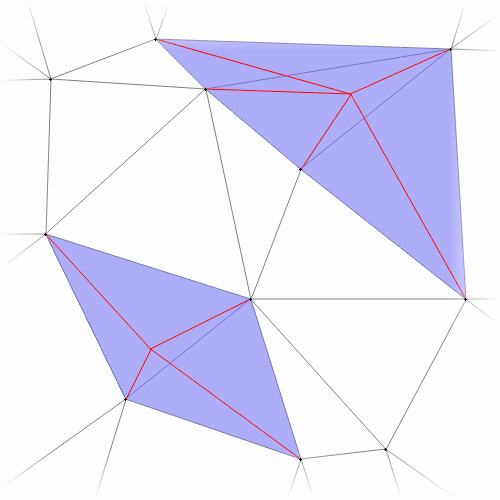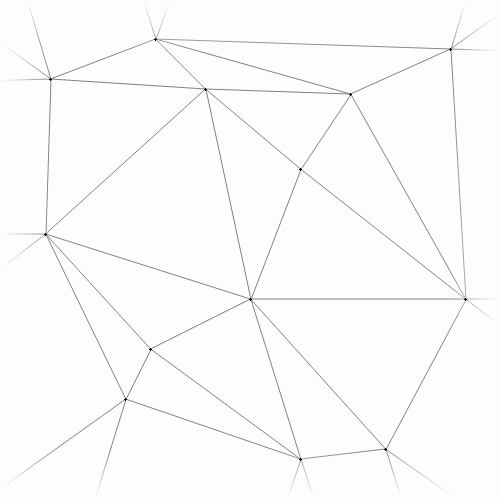
In their paper, Blelloch & friends showed something incredible: if you randomly select a batch of points to insert simultaneously, then the number of overlapping cavities will be small! More specifically, on a mesh of size \(M\) and a sufficiently large (random) batch, there should be about \(O(M)\) points in the batch whose cavities do not overlap.
Below are a couple examples. On the left, in a mesh of size 1000, we see 61 points that can be inserted simultaneously. On the right, 277 points simultaneously inserted into a mesh of size 5000. These examples suggest that on a mesh of size \(M\), we should expect to be able to insert approximately \(M/20\) random points simultaneously.
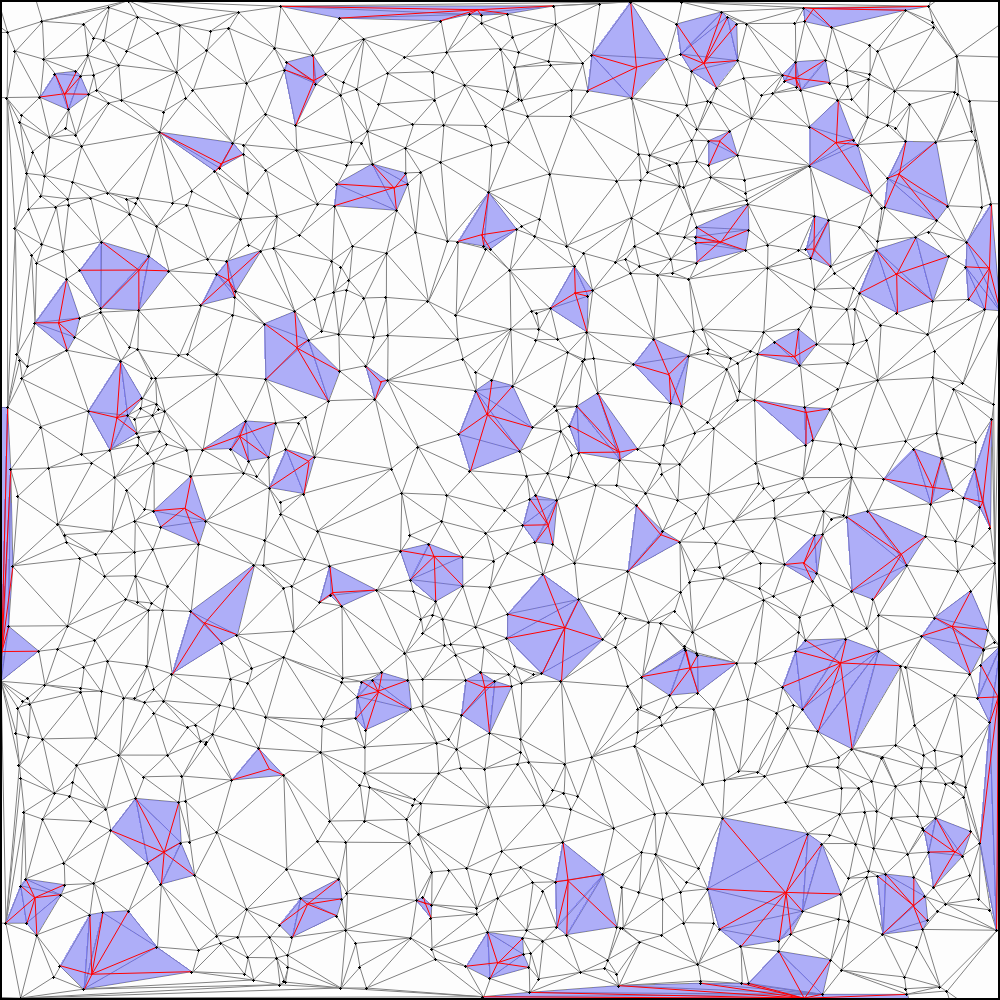 61 insertions into mesh of size 1000 61 insertions into mesh of size 1000 |
 277 insertions into mesh of size 5000 277 insertions into mesh of size 5000 |
Based on the above intuition, here’s the gist of the BGSS algorithm:
- Construct an initial mesh (e.g. a big bounding triangle).
- Repeat until all points have been inserted:
- Let \(M\) be the size of the current mesh.
- Randomly select a batch of \(O(M)\) points to insert.
- Pick a maximal subset of these points such that none of the cavities overlap.
- In parallel, insert these points into the mesh by ripping and tenting.
For \(N\) points overall, this algorithm takes \(O(N \log N)\) work (in expectation) and polylog span (w.h.p.). There are of course quite a few details that I didn’t cover here, like how to efficiently detect overlapping cavities and select a “winner” in these cases. Perhaps I’ll write another post about that in the future. In the meantime, if you’re curious, you could peruse the authors’ code. If you’re curious about performance details, check out this Twitter thread where I describe some of the challenges I encountered when optimizing an implementation for MPL.
Finally, here’s the algorithm running from an initial mesh of size 1K up to a final size of 10K points. Enjoy!